What is Climate Value At Risk (CVaR)?

Source: Built the below explanation by modifying the base article sourced from Philippe Jorion's Orange County Case

(Below article is a 6 mins reading time)

CVaR or Climate Value at Risk is a variation of the standard Value at Risk (VaR). It is important to understand VaR first.

 What is VaR?

VAR summarizes the predicted maximum loss (or worst loss) over a target horizon within a given confidence interval.

How can we compute VAR?

Assume you hold $100 million in medium-term notes. How much could you lose in a month? As much as $100,000? Or $1 million? Or $10 million? Without an answer to this question, investors have no way to decide whether the returns they receive is appropriate compensation for risk.

To answer this question, we first have to analyze the characteristics of medium-term notes. We obtain monthly returns on medium-term bonds from 1953 to 1995. 

                                            Figure  1

 

Returns ranged from a low of -5% to a high of +5.0%. Now construct regularly spaced ``buckets'' going from the lowest to the highest number and count how many observations fall into each bucket. For instance, there is one observation below -5%. There is another observation between -5% and -4.5%. And so on. By so doing, you will construct a ``probability distribution'' for the monthly returns, which counts how many occurrences have been observed in the past for a particular range. 

                                               Figure 2  

For each return, you can then compute a probability of observing a lower return. Pick a confidence level, say 95%. For this confidence level, you can find on the graph a point that is such that there is a 5% probability of finding a lower return. This number is -1.7%, as all occurrences of returns less than -1.7% add up to 5% of the total number of months, or 26 out of 516 months. Note that this could also be obtained from the sample standard deviation, assuming the returns are close to normally distributed.

Therefore, you are now ready to compute the VAR of a $100 million portfolio. There is only a 5% chance that the portfolio will fall by more than $100 million times -1.7%, or $1.7 million. The value at risk is $1.7 million. In other words, the market risk of this portfolio can be communicated effectively to a non-technical audience with a statement such as:

 

Under normal market conditions, the most the portfolio can lose over a month is $1.7 million.

What is the effect of VAR parameters?

In the previous example, VAR was reported at the 95% level over a one-month horizon. The choice of these two quantitative parameters is subjective.

(1) Horizon

For a bank trading portfolio invested in highly liquid currencies, a one-day horizon may be acceptable. For an investment manager with a monthly rebalancing and reporting focus, a 30-day period may be more appropriate. Ideally, the holding period should correspond to the longest period needed for an orderly portfolio liquidation.

(2) Confidence Level

The choice of the confidence level also depends on its use. If the resulting VARs are directly used for the choice of a capital cushion, then the choice of the confidence level is crucial, as it should reflect the degree of risk aversion of the company and the cost of a loss of exceeding VAR. Higher risk aversion, or greater costs, implies that a greater amount of capital should cover possible losses, thus leading to a higher confidence level. In contrast, if VAR numbers are just used to provide a company-wide yardstick to compare risks across different markets, then the choice of the confidence level is not too important.

 

 

Remember: The VaR always calculates the potential loss of an investment with a given time frame and confidence level.

 

How can we convert VAR parameters?

If we are willing to assume a normal distribution for the portfolio returns, then it is easy to convert one horizon or confidence level to another.

As returns across different periods are close to uncorrelated, the variance of a T-day return should be T times the variance of a 1-day return. Hence, in terms of volatility (or standard deviation), Value-at-Risk can be adjusted as:

VAR(T days) = VAR(1 day) x SQRT(T)

Example: Suppose for Variance for 1-day is “v”. So, the variance for 30 days can be calculated as =  v  x square-root(30)

Conversion across confidence levels is straightforward if one assumes a normal distribution. From standard normal tables, we know that the 95% one-tailed VAR corresponds to 1.645 times the standard deviation; the 99% VAR corresponds to 2.326 times sigma; and so on. Therefore, to convert from 99% VAR (used for instance by Bankers Trust) to 95% VAR (used for instance by JP Morgan),

VAR(95%) = VAR(99%) x 1.645 / 2.326.

 

How can you use VAR?

This single number summarizes the portfolio's exposure to market risk as well as the probability of an adverse move. It measures risk using the same units as the bottom line---dollars. Investors can then decide whether they feel comfortable with this level of risk.

If the answer is no, the process that led to the computation of VAR can be used to decide where to trim risk. For instance, the riskiest securities can be sold. Or derivatives such as futures and options can be added to hedge the undesirable risk. VAR also allows users to measure incremental risk, which measures the contribution of each security to total portfolio risk. Overall, it seems that VAR, or some equivalent measure, is an indispensable tool for navigating through financial markets.

 

Let us now try to understand CVaR (Climate Value at Risk)

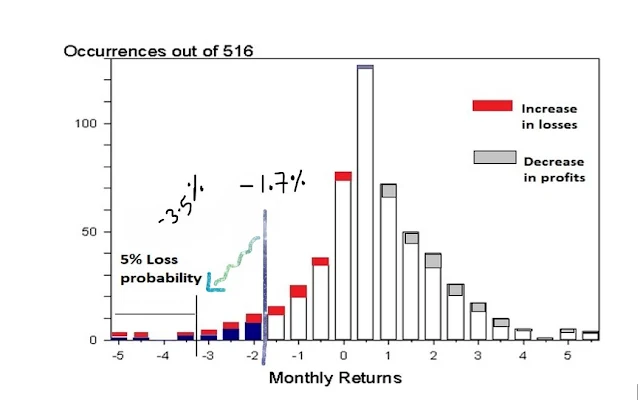
CVaR indicates the impact  of Climate on VaR. Let us extend the example to take into account the losses due to the climate on the profit loss probabilities as indicated in the histogram.  I have modified the histogram as shown below. The difference that you will observe is that I have highlighted the losses increase in red colour. You can treat an increase in loss proportional to the red boxes on top of each of the bar. So, the losses bars indeed resemble lipsticks 😊 While I have shown the profits are decreasing due to the climate impacts as shown in grey areas. Each grey boxes on right hand side of the mean indicate a decrease from the original value. Size of each grey box indicates proportional decrease in profit.

So what is the impact?

Let us again pick a confidence level, say 95%. For this confidence level, you can find on the graph a point that is such that there is a 5% probability of finding a lower return. Due to the increased losses, the point at which we get the sum of lowest 5% shifts to the left. This means in the previous histogram where we had - 1.7% as the point below which we got returns lower than 5% has shifted to about -3.5%.

                                                                          Figure 3

Therefore, you are now again ready to compute the VAR of a $100 million portfolio. There is only a 5% chance that the portfolio will fall by more than $100 million times -3.5%, or $3.5 million.

 

So, it can be said that 95% VaR of the said portfolio is $3.5 million. This means it can be said with 95% confidence that the portfolio of 1 Million USD will not incur losses more than $3.5 million over a month.

So, to end with: Is it good to have a CVaR value as big or as small as possible?

Please share your response in the comment.

Why support?